Treap（树堆）

发表于 更新于 分类于 Valine： 本文字数： 12k 阅读时长 ≈ 10 分钟

最近在LeetCode刷题，又开始复习算法和数据结构，打算写一些东西，记录一些有通用价值的算法和数据结构。

先拿Treap开刀。

什么是Treap？

Treap是一种二叉搜索树（BST），我的本科毕业论文课题就是就是关于二叉搜索树（BST）的研究，Treap在各种操作的效率上不算优秀，全面优秀的是红黑树（RBT），红黑树也是实现起来最复杂的，各种语言的dict，map，set，大概率是基于红黑树实现的，那为什么我讲Treap不讲红黑树呢，因为Treap可能是最易理解且实现起来最简单的且效率还不错的BST，所以经常被用在竞赛中。

Treap支持的操作

1）插入

2）删除

3）查询存在或查询个数

4）查询元素的排名（即元素是第几小，或者说统计 小于/大于 指定元素的个数）

5）查询第 k 小元素

以上5个操作的平均时间复杂度都是O(logn)，

朴素BST的实现

我们先实现一个朴素的BST，为了简化起见：

1）仅支持3种基本操作，insert，erase，count。（名字按C++ STL容器的命名规则取的）

2）只存key而没有value，像set，而不是map。

3）不能插入重复的key，像set，而不是multiset。

4）没写销毁时的内存释放（那并不困难）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
struct TreeNode {
    int key;
    TreeNode* left;
    TreeNode* right;

    TreeNode():TreeNode(0){}
    TreeNode(int key):key(key),left(NULL),right(NULL){}
};

class BST {
public:
    void insert(int key) {
        _insert(root, new TreeNode(key));
    }

    int count(int key) const {
        return _count(root, key);
    }

    void erase(int key) {
        return _erase(root, key);
    }

private:
    void _insert(TreeNode* &root, TreeNode* p) {
        if(root == NULL) {
            root = p;
        } else {
            if(p->key == root->key) return;
            if(p->key < root->key) _insert(root->left, p);
            else _insert(root->right, p);
        }
    }

    bool _count(TreeNode* root, int key) const {
        if(root == NULL) return 0;
        if(key == root->key) return 1;
        if(key < root->key) return _count(root->left, key);
        else return _count(root->right, key);
    }

    void _erase(TreeNode* &root, int key) {
        if(root == NULL) return;
        if(key == root->key) {
            TreeNode* left = root->left;
            TreeNode* right = root->right;
            if(left == NULL) {
                delete root;
                root = right; // 因为左子树为空，直接用右子树当根就可以了
            } else if(right == NULL) {
                delete root;
                root = left;
            } else { // 左右子树都不空，把右孩子作为新根
                delete root;
                root = right;
                TreeNode* p = right; // 找到右子树中最小的节点，把左子树接上去
                while(p->left) { 
                    p = p->left;
                }
                p->left = left;
            }
        } else if(key < root->key) {
            _erase(root->left, key);
        } else {
            _erase(root->right, key);
        }
    }

private:
    TreeNode* root = NULL;
};

其中插入insert和查询count都比较简单，主要讲一下erase操作，当删除的是一个非叶子节点，要考虑如何把删除节点的左右子树接上，如果只有左子树或只有右子树，那么直接取代删除节点作为根就可以了，当左右子树都存在时，左右孩子都可以作为新根，这里选择右孩子作为新根，那么要把左子树接上，接到哪里呢，因为整个左子树都key都是小于右子树的，所以可以接在右子树最小的key的left上，而最小的key就是沿left一直下沉到的叶子。

这种删除处理方式虽然是满足BST的性质的，但是显然容易导致树越来越深，因为每次删除操作都会把一棵子树接到叶子节点上，而且总是接到左测最深处，以至于向链表退化，如果改成每次随机选择左右孩子作为新根都会比这好很多。再来看插入操作，只要升序或降序插入，就相当于一直朝着BST的最右或者最左节点插入，这会导致BST退化成链表，那么它的插入、删除、查询等操作的时间复杂度将退化成O(n)，这是不能接受的。各种不同的BST，其实都是通过增加约束条件，使用额外的维护操作维护约束的满足，来减小BST的最大深度，把平均甚至最坏的深度维持在O(logn)。

Treap是如何克服上述朴素BST的问题的呢？

Treap由二叉树和二叉堆组合形成，名字也因此为 tree 和 heap 的组合，除了记录key之外，它还额外记录一个priority来维持最大堆的性质，即父节点的priority大于等于两个子节点的priority，priority一般随机生成，正因为引入了最大堆的约束，和随机的priority，这棵树就不会在某种精心构造的插入删除序列下退化得很深，期望的深度是O(logn)，插入、删除、查询的期望复杂度也是O(logn)，最坏情况O(n)，依赖于priority的生成，因为priority是随机的所以最坏情况基本不会发生。

那么如何维护最大堆约束的满足呢？

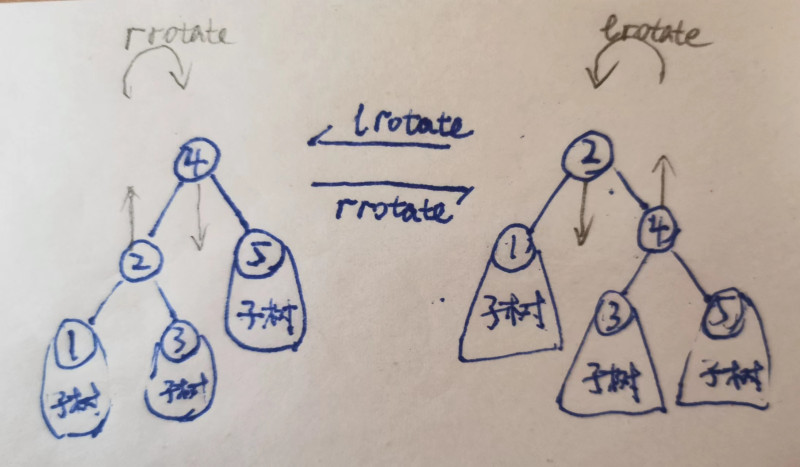
我们需要引入旋转操作，分左旋和右旋，如图所示：

容易看出旋转是不破坏BST性质的，对root右旋用文字描述就是，把root的左孩子作为新根，左孩子的右子树作为旧根的左子树，旧根作为新根的右子树，说起来绕来绕去不好理解，右旋就是把左孩子拎起来成为根，左旋就是把右孩子拎起来成为根，子树的切换是要维持BST性质，想搞错也不容易。

有了不破坏BST性质的旋转操作我们就可以维护堆的性质了，如果左孩子的priority比根大，我们就右旋，让左孩子成为根，如果右孩子的priority比根大，我们就左旋，让右孩子成为根。

Treap的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
struct TreeNode {
    int key;
    int priority;
    TreeNode* left;
    TreeNode* right;

    TreeNode():TreeNode(0){}
    TreeNode(int key):key(key),priority(rand()),left(NULL),right(NULL){}
};

class Treap {
public:
    void insert(int key) {
        _insert(root, new TreeNode(key));
    }

    int count(int key) const {
        return _count(root, key);
    }

    void erase(int key) {
        return _erase(root, key);
    }

private:
    void lrotate(TreeNode* &root) {
        TreeNode* right = root->right;
        //if(right==NULL) return; // 右子树为空不能左旋
        TreeNode* rightleft = right->left;
        root->right = rightleft;
        right->left = root;
        root = right;
    }

    void rrotate(TreeNode* &root) {
        TreeNode* left = root->left;
        //if(left==NULL) return; // 左子树为空不能右旋
        TreeNode* leftright = left->right;
        root->left = leftright;
        left->right = root;
        root = left;   
    }

    void _insert(TreeNode* &root, TreeNode* p) {
        if(root == NULL) {
            root = p;
        } else {
            if(p->key == root->key) return;
            if(p->key < root->key) {
                _insert(root->left, p);
                if(root->left->priority > root->priority){
                    rrotate(root);
                }
            }
            else {
                _insert(root->right, p);
                if(root->right->priority > root->priority){
                    lrotate(root);
                }
            }
        }
    }

    int _count(TreeNode* root, int key) const {
        if(root == NULL) return 0;
        if(key == root->key) return 1;
        if(key < root->key) return _count(root->left, key);
        else return _count(root->right, key);
    }

    void _erase(TreeNode* &root, int key) {
        if(root == NULL) return;
        if(key == root->key) {
            TreeNode* left = root->left;
            TreeNode* right = root->right;
            if(left == NULL) {
                delete root;
                root = right; // 因为左子树为空，直接用右子树当根就可以了
            } else if(right == NULL) {
                delete root;
                root = left;
            } else {
                if(left->priority < right->priority) {
                    rrotate(root); // 把优先级大的孩子转成根
                    _erase(root->right, key);
                } else {
                    lrotate(root);
                    _erase(root->left, key);
                }
            }
        } else if(key < root->key) {
            _erase(root->left, key);
        } else {
            _erase(root->right, key);
        }
    }

private:
    TreeNode* root = NULL;
};

先看插入操作，比朴素BST仅仅多了递归insert后的判断旋转，我们只需关注当前root是否需要旋转，因为这是在递归插入的回退过程中进行的旋转，事实上每次插入都是发生在叶子的，在递归插入回退的过程中新插入的节点会逐层地通过旋转被上推到合适的高度。

再看删除操作，甚至比朴素BST很简洁，在找到需要删除的节点后，我们总是先通过旋转把它下沉，直到它只有一个孩子或者没有孩子，然后再删掉它把孩子接上来。

Treap的完整实现

下面增加了销毁代码，并对动态空间申请释放做了优化，支持插入重复元素，并且实现了另外两个操作：

1）查询元素的排名（即元素是第几小，或者说有多少元素小于指定元素）

2）查询第 k 小元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
#include <iostream>
#include <cassert>
#include <vector>
#include <queue>

using namespace std;

namespace detail {

template <typename T>
struct TreeNode {
    T key;
    int priority;
    int size;
    TreeNode* left;
    TreeNode* right;

    TreeNode():TreeNode(0){}
    TreeNode(T key, int multi=1):key(key),priority(rand()),size(multi),left(NULL),right(NULL){}
};

template <typename T>
class TreeNodePool {
    int batchsize = 1024;
    vector<char*> memchunks;
    queue<char*> blocks;
public:
    ~TreeNodePool() {
        for(int i=0;i<memchunks.size();i++) {
            free(memchunks[i]);
        }
    }

    TreeNode<T>* create(int key, int multi=1) {
        if(blocks.empty()) {
            char* p = (char*)malloc(sizeof(TreeNode<T>)*batchsize);
            memchunks.emplace_back(p);
            for(int i=0;i<batchsize;i++) {
                blocks.push(p+sizeof(TreeNode<T>)*i);
            }
            batchsize *= 2;
        }
        char* p = blocks.front(); blocks.pop();
        return new (p)TreeNode<T>(key, multi);
    }

    void release(TreeNode<T>* p) {
        blocks.push((char*)p);
    }
};
} // namespace detail

template<typename T>
class Treap {
public:
    // key: 插入的元素
    // multi: 插入元素的重数
    int insert(T key, int multi=1) {
        return _insert(root, create_tree_node(key, multi));
    }

    // 返回等于key的元素个数
    int count(T key) const {
        return _count(root, key);
    }

    // key: 删除的元素
    // all: 如果有重复元素是否删除所有
    void erase(T key, bool all=false) {
        _erase(root, key, all);
    }

    // 返回树中元素个数
    int size() const {
        return _size(root);
    }

    // 返回第n小元素，从0起算
    T nth_element(int n) {
        assert(0<=n && n<size());
        return _nth_element(root, n)->key;
    }

    // 返回小于key的元素个数
    int cnt_less(T key) const {
        return _cnt_less(root, key);
    }

    // 返回小于等于key的元素个数
    int cnt_lesseq(T key) const {
        return cnt_less(key) + count(key);
    }

    // 返回大于key的元素个数
    int cnt_greater(T key) {
        return size() - cnt_lesseq(key);
    }

private:
    detail::TreeNode<T>* create_tree_node(T key, int multi=1) {
        return pool.create(key, multi);
    }
    void release_tree_node(detail::TreeNode<T>* root) {
        pool.release(root);
    }

    static int _size(detail::TreeNode<T>* root) {
        return (root != NULL ? root->size : 0);
    }
    // 返回root子树的size减去左右子树的size
    static int _count(detail::TreeNode<T>* root) {
        if(root == NULL) return 0;
        return _size(root) - _size(root->left) - _size(root->right);
    }

    static void lrotate(detail::TreeNode<T>* &root) {
        auto right = root->right;
        assert(right!=NULL);
        auto rightleft = right->left;
        root->right = rightleft;
        right->left = root;
        int root_size = root->size;
        root->size += _size(rightleft) - _size(right);
        right->size = root_size;
        root = right;
    }

    static void rrotate(detail::TreeNode<T>* &root) {
        auto left = root->left;
        assert(left!=NULL);
        auto leftright = left->right;
        root->left = leftright;
        left->right = root;
        int root_size = root->size;
        root->size += _size(leftright) - _size(left);
        left->size = root_size;
        root = left;   
    }

    int _insert(detail::TreeNode<T>* &root, detail::TreeNode<T>* p) {
        if(root == NULL) {
            root = p;
            return p->size;
        } else {
            if(p->key < root->key) {
                int r = _insert(root->left, p);
                root->size += r;
                if(root->left->priority > root->priority){
                    rrotate(root);
                }
                return r;
            } else if(root->key < p->key) {
                int r = _insert(root->right, p);
                root->size += r;
                if(root->right->priority > root->priority){
                    lrotate(root);
                }
                return r;
            } else {
                root->size += p->size;
                release_tree_node(p);
                return p->size;
            }
        }
    }

    static int _count(detail::TreeNode<T>* root, T key) {
        if(root == NULL) return 0;
        if(key < root->key) return _count(root->left, key);
        else if(root->key < key) return _count(root->right, key);
        else return _count(root);
    }

    int _erase(detail::TreeNode<T>* &root, T key, bool all) {
        if(root == NULL) return 0;
        if(key == root->key) {
            auto left = root->left;
            auto right = root->right;
            if(left == NULL) {
                int root_count = _count(root);
                if(!all && root_count > 1) {
                    root->size--;
                    return 1;
                } else {
                    release_tree_node(root);
                    root = right;
                    return root_count;
                }
            } else if(right == NULL) {
                int root_count = _count(root);
                if(!all && root_count > 1) {
                    root->size--;
                    return 1;
                } else {
                    release_tree_node(root);
                    root = left;
                    return root_count;
                }
            } else {
                int root_count = _count(root);
                if(!all && root_count > 1) {
                    root->size--;
                    return 1;
                } else {
                    int r = 0;
                    if(left->priority < right->priority) {
                        lrotate(root); // 把优先级大的孩子转成根
                        r = _erase(root->left, key, all);
                    } else {
                        rrotate(root);
                        r = _erase(root->right, key, all);
                    }
                    root->size -= r;
                    return r;
                }
            }
        } else if(key < root->key) {
            int r = _erase(root->left, key, all);
            root->size -= r;
            return r;
        } else {
            int r = _erase(root->right, key, all);
            root->size -= r;
            return r;
        }
    }

    static int _cnt_less(detail::TreeNode<T>* root, T key) {
        if(root == NULL) return 0;
        if(key < root->key) return _cnt_less(root->left, key);
        else if(root->key < key) return _size(root) - _size(root->right) + _cnt_less(root->right, key);
        else return _size(root->left);
    }

    static detail::TreeNode<T>* _nth_element(detail::TreeNode<T>* root, int n) {
        if(root == NULL) return NULL;
        int left_size = _size(root->left);
        int right_size = _size(root->right);
        if(n < left_size) return _nth_element(root->left, n);
        else if(n < _size(root) - right_size) return root;
        else return _nth_element(root->right, n - (_size(root) - right_size));
    }

private:
    detail::TreeNodePool<T> pool;
    detail::TreeNode<T>* root = NULL;
};