SegTree（线段树）

发表于 更新于 分类于 Valine： 本文字数： 11k 阅读时长 ≈ 10 分钟

什么是线段树？

线段树是一棵二叉树，每个节点维护一个区间和区间上的值，是一种用来维护 区间信息 的数据结构。

我们先从线段树能提供的操作上来理解。想象一个数组，每个下标上可以存一个值。所谓区间就是一段连续的数组下标。

我们可以进行的操作有：

1）区间赋值：设置一个区间内所有下标对应的值

2）单点赋值：设置单点的值

3）区间查询：查询一个区间内的最大值 / 最小值 / 值的和

4）单点查询：查询一个点的值

如果用数组来实现上述操作，所有区间操作的时间复杂度都是O(n)，n是区间长度，单点操作的复杂度都是O(1)，而线段树可以把上述全部操作的时间复杂度同时变成O(logn)

线段树的实现

根据维护的信息和支持的操作不同线段树分很多种，常用的有：着色线段树、覆盖线段树、求和线段树、最值线段树。

计数线段树：可以对区间反复覆盖，动态查询单点的覆盖次数。

着色线段树：可以对区间反复着色，动态查询单点的颜色。

求和线段树：可以对单点或区间赋值，动态查询区间数据的和。

最值线段树：可以对单点或区间赋值，动态查询区间数据的最值。

为了方便起见我用求和线段树进行讲解，并且只实现两种操作：

1）对单点赋值。

2）查询区间和。

假设我们有一个数组

1
arr = {3, 8, 3, 3, 5, 6, 8, 7};

通常情况比如我们求区间[2,7)的和需要遍历区间上的元素，O(区间长度)，如何减少运算次数呢，最简单的思路是我们预处理前缀和sum[]，令

1
sum[i]= arr[0]+arr[1]+...+arr[i-1]

当我们需要算[2,7)的区间和，其实就算[0,7)前缀和减去[0,2)的前缀和，即sum[7]-sum[2]，这样就可以用O(1)的时间算出任意区间的和，如果数组元素不会发生动态变化这样是可以的，但如果需要交替修改数组元素和查询区间和，这样处理会导致前缀和维护的成本很高，原本的arr[i]=x，我们不得不修改所有k>i的sum[k]来维护前缀和，这样修改数组元素的时间就从原本的O(1)变成了O(n)。

有没有方法可以在修改单点值的便利性和查询区间和的便利性上做个折中呢，肯定是有的，我们可以预处理一些子段和而不是所有前缀和，让修改单点值和查询区间和都只需要访问O(logn)的元素，树状数组和线段树都是类似这个思想，其实树状数组的设计更符合这个思想，但它只能用于求和，树状数组能做的线段树都能做，我们之后有空再讲树状数组，对于线段树我们先在这个数组上生成一个子段和数组，让

1
b = { arr[0]+arr[1],  arr[2]+arr[3], arr[4]+arr[5], arr[6]+arr[7]} = {11, 6, 11, 15};

这样求区间[2, 7)的和的时候，可以取b[1] + b[2] + arr[6]，只需要算三个数的和就行了。

更近一步，我们可以在数组b上再合并建立 c = { b[0]+ b[1], b[2]+b[3], …}, d, e, …，直至把整个数组合并成一个元素，如下图

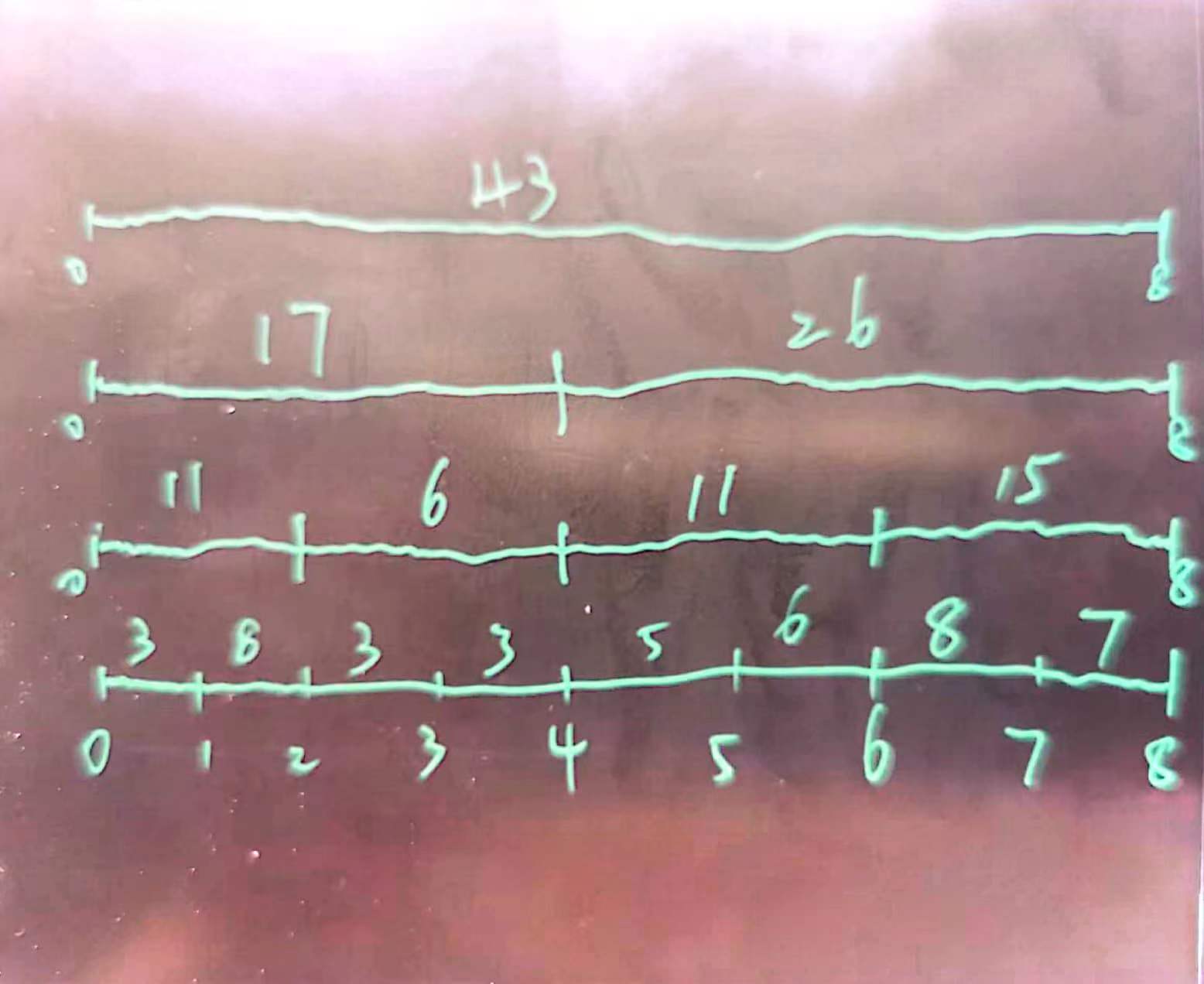
segtree

这样之后，对于这个数组上的任意区间的和都可以只取O(logn)的元素的和来得到。

为了方便，我们通过二叉树来维护这些数据，我们把最上面的整个数组的和43作为二叉树的根，同时记住这个节点对应的左右端点即0和8，我们把这个节点的数据表示为（0, 8, 43），然后把它的左孩子就是如图的和为17的节点，数据为(0, 4, 17)，同理右孩子(4, 8, 26)，以此类推，这样就可以建立一颗完全二叉树（我这里有意将数组的大小选为2的幂，如果不是2的幂我们也可以扩充到2的幂来建树）。

对于修改单点值的操作，我们要从树根一直修改到叶子，正好修改了树的深度个节点，复杂度也是O(logn)。

因为是完全二叉树，我们可以通过数组来实现，用data[0]作为根，data[k]的孩子是data[2*k+1]和data[2*k+2]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <iostream>
using namespace std;

#define MAXN 8
int bg[MAXN*2]; // 区间左端点，闭
int nd[MAXN*2]; // 区间右端点，开
int sm[MAXN*2]; // 节点值，即区间和

// 递归构建树
void build(int k, int b, int e) {
    bg[k] = b;
    nd[k] = e;
    sm[k] = 0;
    if(e-b>1) {
        int mid = b + (e-b) / 2;
        build(k*2+1, b, mid);
        build(k*2+2, mid, e);
    }
}

// 设置数组下标i的元素值，类似arr[i] = val
void change(int k, int i, int val) {
    if(nd[k]-bg[k]==1) { // 叶子节点
        sm[k] = val; // 直接更新
    } else {
        int mid = bg[k] + (nd[k]-bg[k]) / 2;
        // 递归向下更新
        if(i<mid) change(k*2+1, i, val);
        else change(k*2+2, i, val);
        // 回溯时通过孩子的值更新当前节点值
        sm[k] = sm[k*2+1] + sm[k*2+2];
    }
}

// 查询[b, e)的元素和
int query(int k, int b, int e) {
    if(b<=bg[k] && nd[k]<=e) {
        cout << "DEBUG:[" << bg[k] << "," << nd[k] << ") sm[k]=" << sm[k] << endl;
        return sm[k];
    }
    int mid = bg[k] + (nd[k]-bg[k]) / 2;
    return (b<mid ?query(k*2+1, b, e):0) + (mid<e ? query(k*2+2, b, e):0);
}

// 把n向上对齐到2的幂
int align(int n) {
    if(n & (n-1)) {
        while(n & (n-1)) {
            n &= (n-1);
        }
        n = (n << 1);
    }
    return n;
}

int main()
{
    int arr[] = {3,8,3,3,5,6,8,7};
    build(0, 0, align(8));
    for(int i=0;i<8;i++) {
        change(0, i, arr[i]);
    }
    cout << query(0, 2, 7) << endl;
}

输出

1
2
3
4
DEBUG:[2,4) sm[k]=6
DEBUG:[4,6) sm[k]=11
DEBUG:[6,7) sm[k]=8
25

可以看到，和预期的一样，只通过3个节点的值求和算出了区间[2,7)的和为25。

最值线段树

对于最大值、最小值的线段树，我们只需要把更新节点值的代码改掉。

区间更新

对于区间更新，例如把[a,b)的值全部设置为x，或者让[a,b)的值全部增加x，我们不能对区间内的点逐一更新，否则复杂度会变成O(nlogn)了，区间更新时，我们要引入懒惰标志，我们还是从根开始拆分区间，如果当前节点的区间被完全覆盖，我们就更新当前节点值并不向下继续更新，并把待更新的值记在懒惰标志内，直到查询需要用到节点值时再逐级更新并把懒惰标志一层层推下去。

离散化

我们可以看到上述线段树实现方式使用的数据空间是数组最大下标的2倍，有时候区间的范围很大，但区间的更新和查询操作的数量并不多，我们可以先统计所有的区间端点，比如有n个端点，然后排序，在所有区间端点和 0,1,…,n-1 之间做一一映射，然后就可以把线段树的空间降到 2*n，和区间个数相关而和区间范围无关。

动态开点

我们也可以不用数组表示的完全二叉树来实现线段树，而用一棵记录左右孩子指针的动态申请空间的普通二叉树，根据更新的区间来动态生成区间节点，这一般被称作动态开点。

支持区间更新的最大值线段树的完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168

const int INF = 1e9+7;

// 最大值线段树
class SegTree {
    vector<int> nums;
    vector<int> d;
    vector<int> b;  // lazy
    vector<bool> v; // true: b中是设置值 false: b中是增量值

    void build(int s, int t, int p = 1) {
        // 对 [s,t] 区间建立线段树,当前根的编号为 p
        if (s == t) {
            d[p] = nums[s];
            return;
        }
        int m = s + ((t - s) >> 1);
        // 移位运算符的优先级小于加减法，所以加上括号
        // 如果写成 (s + t) >> 1 可能会超出 int 范围
        build(s, m, p * 2);
        build(m + 1, t, p * 2 + 1);
        // 递归对左右区间建树
        d[p] = std::max(d[p * 2], d[(p * 2) + 1]);
    }

    // [l, r] 为修改区间, c 为被修改的元素的变化量, [s, t] 为当前节点包含的区间, p
    // 为当前节点的编号
    void add(int l, int r, int c, int s, int t, int p) {
        // 当前区间为修改区间的子集时直接修改当前节点的值,然后打标记,结束修改
        if (l <= s && t <= r) {
            if(v[p]) {
                pushdown(s, t, p);
            }
            d[p] += c;
            b[p] += c;
            v[p] = 0;
            return;
        }
        pushdown(s, t, p);
        int m = s + ((t - s) >> 1);
        if (l <= m) add(l, r, c, s, m, p * 2);
        if (r > m) add(l, r, c, m + 1, t, p * 2 + 1);
        d[p] = std::max(d[p * 2], d[p * 2 + 1]);
    }

    // [l, r] 为修改区间, c 为被修改的元素的值, [s, t] 为当前节点包含的区间, p
    // 为当前节点的编号
    void set(int l, int r, int c, int s, int t, int p) {
        if (l <= s && t <= r) {
            d[p] = c;
            b[p] = c;
            v[p] = 1;
            return;
        }
        pushdown(s, t, p);
        int m = s + ((t - s) >> 1);
        if (l <= m) set(l, r, c, s, m, p * 2);
        if (r > m) set(l, r, c, m + 1, t, p * 2 + 1);
        d[p] = std::max(d[p * 2], d[p * 2 + 1]);
    }

    void pushdown(int s, int t, int p) {
        if(v[p]) { // 如果是设置值
            d[p * 2] = b[p];
            d[p * 2 + 1] = b[p];
            // 设置值可以清掉增量值而不用管之前b中是否有待增量懒值
            b[p * 2] = b[p * 2 + 1] = b[p];
            v[p * 2] = v[p * 2 + 1] = 1;
            b[p] = 0;
            v[p] = 0;
        } else { // 如果是增量值
            if(b[p]) {
            	int m = s + ((t - s) >> 1);
                // 如果子节点有待设置的懒值
                if(v[p * 2]) {
                    pushdown(s, m, p * 2);
                }
                if(v[p * 2 + 1]) {
                    pushdown(m + 1, t, p * 2 + 1);
                }
                // 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
                d[p * 2] += b[p];
                d[p * 2 + 1] += b[p];
                b[p * 2] += b[p];
                b[p * 2 + 1] += b[p];  // 将标记下传给子节点
                b[p] = 0;              // 清空当前节点的标记
            }
        }
    }

    int getmax(int l, int r, int s, int t, int p) {
        // [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p 为当前节点的编号
        if (l <= s && t <= r) return d[p];
        // 当前区间为询问区间的子集时直接返回当前区间的和
        int m = s + ((t - s) >> 1);
        pushdown(s, t, p);
        int max_value = -INF;
        if (l <= m) max_value = std::max(max_value, getmax(l, r, s, m, p * 2));
        if (r > m) max_value = std::max(max_value, getmax(l, r, m + 1, t, p * 2 + 1));
        return max_value;
    }
public:
    SegTree(int size): nums(size) {
        d.resize(size*4);
        b.resize(size*4);
        v.resize(size*4);
        build(0, nums.size()-1, 1);
    }

    SegTree(const vector<int>& a): nums(a) {
        d.resize(a.size()*4);
        b.resize(a.size()*4);
        v.resize(a.size()*4);
        build(0, nums.size()-1, 1);
    }

    // 对区间[b, e)的值增加c
    void add(int b, int e, int c) {
        add(b, e-1, c, 0, nums.size()-1, 1);
    }

    // 将区间[b, e)的值设置为c
    void set(int b, int e, int c) {
        set(b, e-1, c, 0, nums.size()-1, 1);
    }

    // 得到区间[b, e)上的最大值
    int max(int b, int e) {
        if(e<=b) return -INF;
        return getmax(b, e-1, 0, nums.size()-1, 1);
    }

private:
    class ItemAccessor {
    public:
        ItemAccessor(SegTree& st, int i): st(st), i(i) {}
        ItemAccessor& operator = (int x) {st.set(i, i+1, x);return *this;}
        ItemAccessor& operator += (int x) {st.add(i, i+1, x);return *this;}
        ItemAccessor& operator -= (int x) {st.add(i, i+1, x);return *this;}
        operator int() const {return st.max(i, i+1);}
    private:
        SegTree& st;
        int i;
    };

    class RangeAccessor {
    public:
        RangeAccessor(SegTree& st, int b, int e):st(st), b(b), e(e) {}
        void operator = (int x) {st.set(b, e, x);}
        void operator += (int x) {st.add(b, e, x);}
        void operator -= (int x) {st.add(b, e, x);}
    private:
        SegTree& st;
        int b;
        int e;
    };

public:
    // 通过下标访问单点值的语法糖
    ItemAccessor operator [] (int i) {
        return ItemAccessor(*this, i);
    }

    // 通过下标访问区间值的语法糖
    RangeAccessor operator [] (const tuple<int, int>& range) {
        return RangeAccessor(*this, std::get<0>(range), std::get<1>(range));
    }
};

支持区间更新的求和线段树的完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
const int INF = 1e9+7;

// 求和线段树
class SegTree {
    vector<int> nums;
    vector<int> d;
    vector<int> b;  // lazy
    vector<bool> v; // true: b中是设置值 false: b中是增量值

    void build(int s, int t, int p = 1) {
        // 对 [s,t] 区间建立线段树,当前根的编号为 p
        if (s == t) {
            d[p] = nums[s];
            return;
        }
        int m = s + ((t - s) >> 1);
        // 移位运算符的优先级小于加减法，所以加上括号
        // 如果写成 (s + t) >> 1 可能会超出 int 范围
        build(s, m, p * 2);
        build(m + 1, t, p * 2 + 1);
        // 递归对左右区间建树
        d[p] = d[p * 2] + d[(p * 2) + 1];
    }

    // [l, r] 为修改区间, c 为被修改的元素的变化量, [s, t] 为当前节点包含的区间, p
    // 为当前节点的编号
    void add(int l, int r, int c, int s, int t, int p) {
        // 当前区间为修改区间的子集时直接修改当前节点的值,然后打标记,结束修改
        if (l <= s && t <= r) {
            if(v[p]) {
                pushdown(s, t, p);
            }
            d[p] += c * (t - s + 1);
            b[p] += c;
            v[p] = 0;
            return;
        }
        pushdown(s, t, p);
        int m = s + ((t - s) >> 1);
        if (l <= m) add(l, r, c, s, m, p * 2);
        if (r > m) add(l, r, c, m + 1, t, p * 2 + 1);
        d[p] = d[p * 2] + d[p * 2 + 1];
    }

    // [l, r] 为修改区间, c 为被修改的元素的值, [s, t] 为当前节点包含的区间, p
    // 为当前节点的编号
    void set(int l, int r, int c, int s, int t, int p) {
        if (l <= s && t <= r) {
            d[p] = c * (t - s + 1);
            b[p] = c;
            v[p] = 1;
            return;
        }
        pushdown(s, t, p);
        int m = s + ((t - s) >> 1);
        if (l <= m) set(l, r, c, s, m, p * 2);
        if (r > m) set(l, r, c, m + 1, t, p * 2 + 1);
        d[p] = d[p * 2] + d[p * 2 + 1];
    }

    void pushdown(int s, int t, int p) {
    	int m = s + ((t - s) >> 1);
        if(v[p]) { // 如果是设置值
            d[p * 2] = b[p] * (m - s + 1);
            d[p * 2 + 1] = b[p] * (t - m);
            // 设置值可以清掉增量值而不用管之前b中是否有待增量懒值
            b[p * 2] = b[p * 2 + 1] = b[p];
            v[p * 2] = v[p * 2 + 1] = 1;
            b[p] = 0;
            v[p] = 0;
        } else { // 如果是增量值
            if(b[p]) {
                // 如果子节点有待设置的懒值
                if(v[p * 2]) {
                    pushdown(s, m, p * 2);
                }
                if(v[p * 2 + 1]) {
                    pushdown(m + 1, t, p * 2 + 1);
                }
                // 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
                d[p * 2] += b[p] * (m - s + 1);
                d[p * 2 + 1] += b[p] * (t - m);
                b[p * 2] += b[p];
                b[p * 2 + 1] += b[p];  // 将标记下传给子节点
                b[p] = 0;              // 清空当前节点的标记
            }
        }
    }

    int getsum(int l, int r, int s, int t, int p) {
        // [l, r] 为查询区间, [s, t] 为当前节点包含的区间, p 为当前节点的编号
        if (l <= s && t <= r) return d[p];
        // 当前区间为询问区间的子集时直接返回当前区间的和
        int m = s + ((t - s) >> 1);
        pushdown(s, t, p);
        int sum = 0;
        if (l <= m) sum += getsum(l, r, s, m, p * 2);
        if (r > m) sum += getsum(l, r, m + 1, t, p * 2 + 1);
        return sum;
    }
public:
    SegTree(int size): nums(size) {
        d.resize(size*4);
        b.resize(size*4);
        v.resize(size*4);
        build(0, nums.size()-1, 1);
    }

    SegTree(const vector<int>& a): nums(a) {
        d.resize(a.size()*4);
        b.resize(a.size()*4);
        v.resize(a.size()*4);
        build(0, nums.size()-1, 1);
    }

    // 对区间[b, e)的值增加c
    void add(int b, int e, int c) {
        add(b, e-1, c, 0, nums.size()-1, 1);
    }

    // 将区间[b, e)的值设置为c
    void set(int b, int e, int c) {
        set(b, e-1, c, 0, nums.size()-1, 1);
    }

    // 得到区间[b, e)上的值的和
    int sum(int b, int e) {
    	if(e<=b) return 0;
        return getsum(b, e-1, 0, nums.size()-1, 1);
    }

private:
    class ItemAccessor {
    public:
        ItemAccessor(SegTree& st, int i): st(st), i(i) {}
        ItemAccessor& operator = (int x) {st.set(i, i+1, x);return *this;}
        ItemAccessor& operator += (int x) {st.add(i, i+1, x);return *this;}
        ItemAccessor& operator -= (int x) {st.add(i, i+1, x);return *this;}
        operator int() const {return st.sum(i, i+1);}
    private:
        SegTree& st;
        int i;
    };

    class RangeAccessor {
    public:
        RangeAccessor(SegTree& st, int b, int e):st(st), b(b), e(e) {}
        void operator = (int x) {st.set(b, e, x);}
        void operator += (int x) {st.add(b, e, x);}
        void operator -= (int x) {st.add(b, e, x);}
    private:
        SegTree& st;
        int b;
        int e;
    };

public:
    // 通过下标访问单点值的语法糖
    ItemAccessor operator [] (int i) {
        return ItemAccessor(*this, i);
    }

    // 通过下标访问区间值的语法糖
    RangeAccessor operator [] (const tuple<int, int>& range) {
        return RangeAccessor(*this, std::get<0>(range), std::get<1>(range));
    }
};