Binary Indexed Tree（树状数组）

发表于 更新于 分类于 Valine： 本文字数： 2.7k 阅读时长 ≈ 2 分钟

什么是树状数组？

树状数组又称二叉索引树(Binary Indexed Tree)，又以其发明者命名为Fenwick树。

是一种支持以O(logn)时间计算区间和同时以O(logn)时间修改元素值的数据结构。

它的功能可以被线段树替代，而且线段树提供了更多功能，树状数组的优势是实现简单。

树状数组的的实现

树状数组提供两种操作：

1）对单点赋值。

2）查询区间和。

（事实上也可以扩展出区间修改和单点查询，我们暂不考虑）

假设我们有一个数组

1
arr = {3, 8, 3, 3, 5, 6, 8, 7};

通常情况比如我们求区间[2,7)的和需要遍历区间上的元素，O(区间长度)，如何减少运算次数呢，最简单的思路是我们预处理前缀和sum[]，令

1
sum[i]= arr[0]+arr[1]+...+arr[i-1]

当我们需要算[2,7)的区间和，其实就算[0,7)前缀和减去[0,2)的前缀和，即sum[7]-sum[2]，这样就可以用O(1)的时间算出任意区间的和，如果数组元素不会发生动态变化这样是可以的，但如果需要交替修改数组元素和查询区间和，这样处理会导致前缀和维护的成本很高，原本的arr[i]=x，我们不得不修改所有k>i的sum[k]来维护前缀和，这样修改数组元素的时间就从原本的O(1)变成了O(n)。

有没有方法可以在修改单点值的便利性和查询区间和的便利性上做个折中呢，肯定是有的，我们可以预处理一些子段和而不是所有前缀和，让修改单点值和查询区间和都只需要访问O(logn)的元素，树状数组和线段树都是类似这个思想。

这是在讲线段树时的图，如果我们只考虑前缀和，即从0开始的区间和，这中间很多子段和的存储是不必要的，我们来看[0, 7)的和，如果我们有了下图维护的子段和信息，[0, 7)的和最快可以通过 [0, 4)的和 + [4, 6)的和 + [6,7)的和 = 17 + 11 + 8 计算得到。

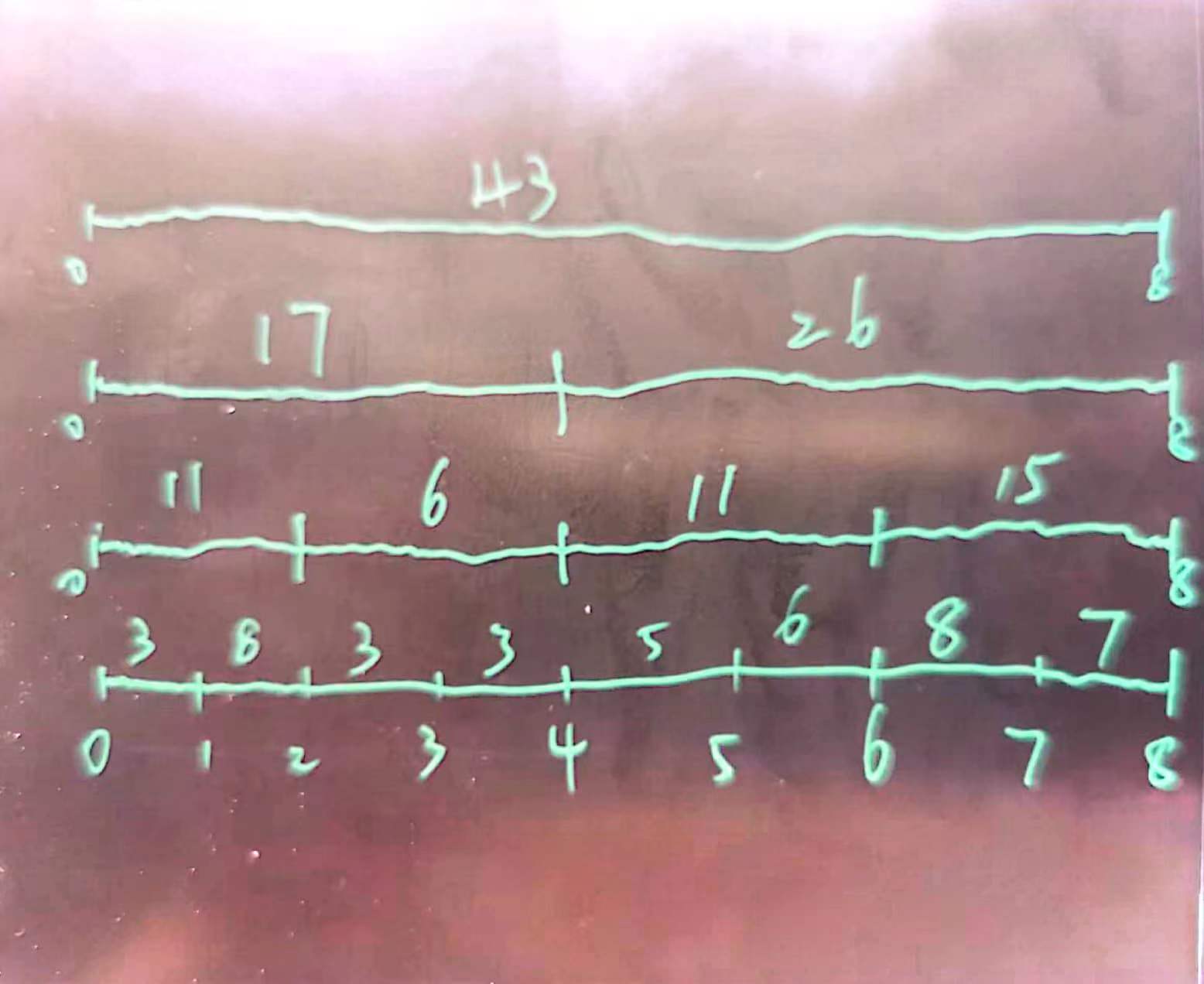
segtree

我们看图时是很容易想到的，那么这个[0, 4)、[4, 6)、[6,7)划分是怎么得出来的呢，我们可以把前缀和[0, 7)的右端点7转换成2进制，即111，如果仅保留最左侧的1其他位置0，得到100，就是十进制的4，保留最左侧的两个1，得到110，就是十进制的6，保留最最侧的三个1，得到111，就是十进制的7。4,6,7 正好和我们的划分是一样的。7并不是特殊的，可以选择其他数字也都有这个规律。那么给定一个i，我们就可以通过不断把最右侧1变成0，记录这个过程中所有的数，就可以得到需要用到的子段和的划分。具体操作方式我们可以通过位运算。

1
2
3
4
// 得到n二进制最右侧的1表示的数
int lowbit(int n) {
    return n & (-n);
}

还有一些等价的写法

1
n & ~(n-1) 或 n ^ (n & (n-1))

划分子段和的方式有了，刚才提到如果我们只计算前缀和，线段树维护的这些子段很多是多余的，再结合我们的划分方式，其实只要把子段和存储在子段的右端点即可。需要用到的子段右端点是不会重复的，因为任何一个右端点i 对应唯一子段就是 [k , i)，其中k是i的二进制去掉最右的1。也就是下面这样，虚线上方圆圈内的值就是存储在右端点的子段和。

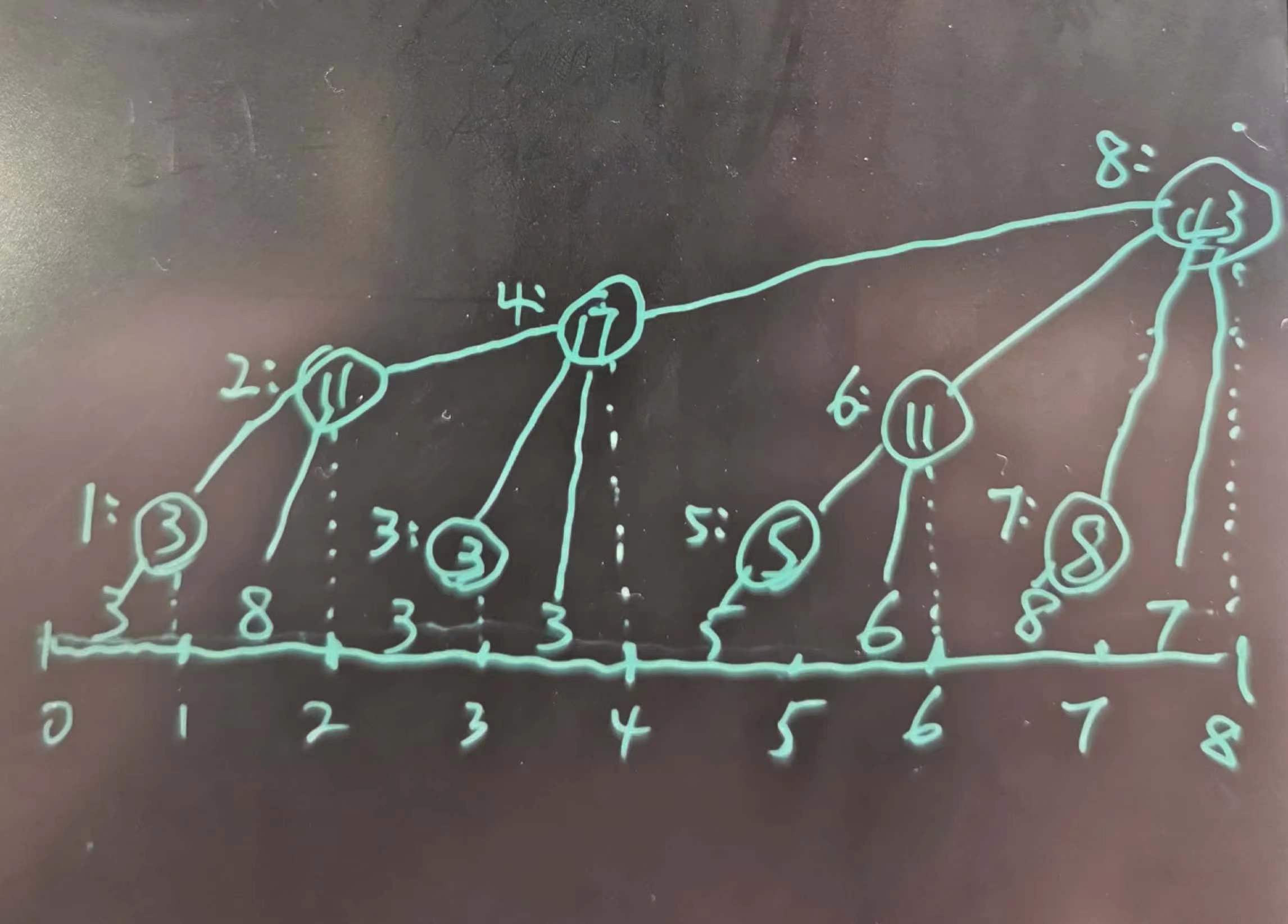
bitree

那么我们就可以仅用一个数组来存储上面的这棵树了。

1
2
bitree[] = {0, 3, 11, 3, 17, 5, 11, 8, 43};
            0  1   2  3   4  5   6  7   8

实际上这里 len(bitree) = len(arr) + 1，不过bitree[0] 代表空的子段和，总是0，想省下多出来的1个单位空间也是可以的，不过没有必要。

所以求任意的区间和，我们先转成前缀和相减，再划分为子段和去bitree[]里取值就可以了

例如：

1
2
3
4
5
  [2, 7)的和
= [0, 7)的和 - [0, 2)的和
= (bitree[4] + bitree[6] + bitree[7]) - bitree[2]
= (17 + 11 + 8) - 11
= 25

用代码实现就是

1
2
3
4
5
6
7
8
9
// 查询前缀和
int query(int i) {
    int result = 0;
    while(i) {
        result += bitree[i];
        i -= lowbit(i); // 等价的 i &= i-1 
    }
    return result;
}

剩下的问题是如何修改元素值呢？我们看上面的树状图，当要修改元素4的时候，会影响到[4,5)、[4,6)，[0,8) 三个区间，即一直要沿着父节点修改到根，那么就是我们用bitree的下标表示就是5-6-8，如何得到这一串数呢，是否也和二进制存在某种关系呢，直接说答案，从要修改的元素编号+1开始，每次令i+=lowbit(i) 得到下个序号（正好是把查询里的减法变成加法），直到下标超出bitree的长度，事实上最后一次的下标总是bitree的根，也就是最后一个的元素。

1
2
3
4
5
6
7
8
// 修改元素i的值
void add(int i, int x) {
    ++i;
    while(i<=8) {
        bitree[i] += x;
        i += lowbit(i);
    }
}

这里实现的是add方法，如果我们想设置元素i为新值，可以

1
2
add(i, -query(i,i+1)); // 减去旧值
add(i, x); // 加上新值

完整实现

和线段树比一下是不是简单很多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
template <typename T, int N=(1<<17)>
class BITree{
    T C[N+1];
    int lowbit(int i){return i&(-i);}
public:
    BITree(){clear();}

    void clear(){memset(C,0,sizeof(C));}

    // 增量修改元素i的值
    void add(int i, T d){
        for(i++; i<=N; i+=lowbit(i)) C[i]+=d;
    }
    
    // [0, i)元素的和
    T sum(int i){
        T r=0;
        for(; i; i-=lowbit(i)) r+=C[i];
        return r;
    }

    // [b, e)元素的和
    T sum(int b, int e) {
        return sum(e) - sum(b);
    }

    // 修改元素i的值
    void set(int i, T d) {
        add(i, -sum(i, i+1));
        add(i, d);
    }
};