凸包

发表于 更新于 分类于 Valine： 本文字数： 1.4k 阅读时长 ≈ 1 分钟

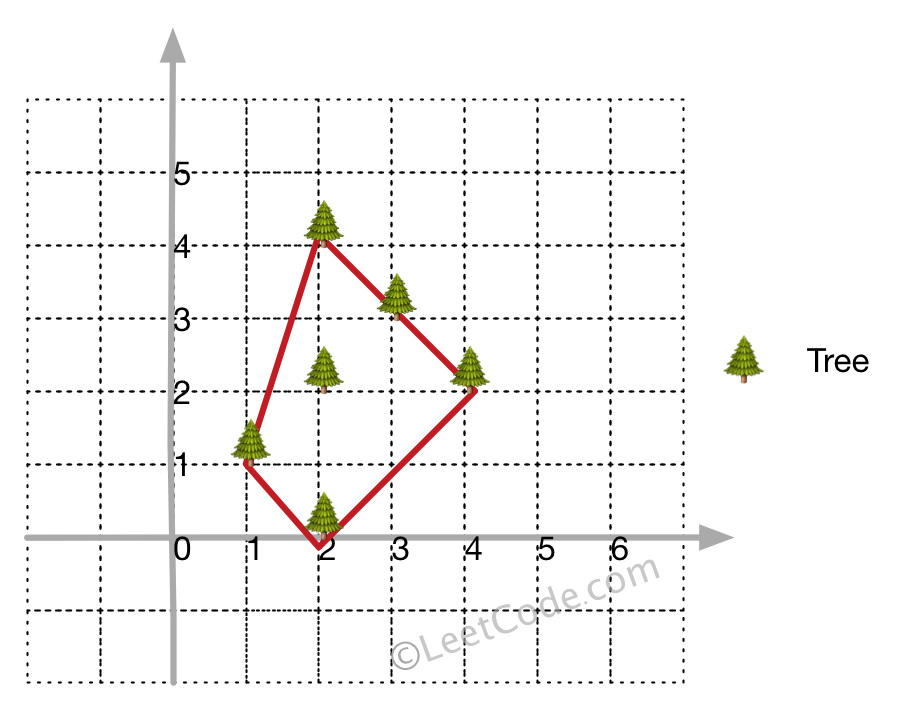
给定二维平面内的一组点集，求出包住所有点的最小的凸多边形。

1
2
输入: [(1, 1), (2, 2), (2, 0), (2, 4), (3, 3), (4, 2)]
输出: [(4, 2), (2, 4), (1, 1), (2, 0)]

算法思路是先排序（优先按x轴），然后分别求出上下包围线，从左到右遍历的过程使用单调栈维护包围线，包围线只能向同一侧弯曲（上包围线向下弯曲，上包围线向下弯曲），用叉乘计算连续两个线段的弯曲方向（二维向量其实是拟叉乘，三维向量的叉乘结果应该是一个向量，屏幕上两向量叉乘是一个指向屏幕外或屏幕内的向量，这里只用一个带正负的值表示方向和长度，其实我们这里也只用到方向）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 二维向量
struct v2d {
    double x;
    double y;
};

// 二维向量拟叉积运算
double pseudoCross(const v2d& v1, const v2d& v2) {
    return v1.x * v2.y - v1.y * v2.x;
}

v2d operator - (const v2d& v1, const v2d& v2) {
    return v2d{v1.x-v2.x, v1.y-v2.y};
}

// 返回一个逆时针围成的凸包（如果要顺时针可以把上下边界换一换，改变while中的比较就可以）
vector<v2d> convexHull(vector<v2d>& pnts) {
    sort(pnts.begin(), pnts.end(), [](const v2d& v1, const v2d& v2) {
        return ((v1.x != v2.x)?(v1.x< v2.x):(v1.y < v2.y));
    });
    int n = pnts.size();
    vector<int> v(n*2); // v 其实是两个单调栈在中间接起来
    int p = n; // 从v中间向后增长的单调栈, p为栈顶的下一个位置（将要被使用的空间）
    int q = n; // 从v中间向前增长的单调栈, q为栈顶的下一个位置（将要被使用的空间）
    for(int i=0; i<n; i++){
        while(p-n>=2 && pseudoCross(pnts[i]-pnts[v[p-1]], pnts[v[p-1]]-pnts[v[p-2]])>=0){
            p--; // 弯曲方向不对，出栈
        }
        while(n-q>=2 && pseudoCross(pnts[i]-pnts[v[q+1]], pnts[v[q+1]]-pnts[v[q+2]])<=0){
            q++; // 弯曲方向不对，出栈
        }
        v[p++] = i;
        v[q--] = i;
    }
    vector<v2d> res;
    for(int i=q+1;i<p-1;i++) {
        res.push_back(pnts[v[i]]);
    }
    return res;
}