RMQ问题-ST算法

问题描述

RMQ问题即区间最值查询问题（Range Minimum/Maximum Query）

给定一个数组，大量的查询区间的最值，我们知道如果数组长度是n，有n*(n-1)/2个不同区间，如果只有少量的查询我们可以遍历区间的元素，算法的时间复杂度显然是O(len) len是区间长度，对于随机的区间一次查询的复杂度也就是O(n)。

如果查询的次数增加到n^{2数量级，我们可以用递推预处理出所有区间的最值，预处理时间O(n}2)，查询时间O(1)。

如果查询的次数和n是同等量级，无论我们采取遍历还是预处理所有区间总体时间都是O(n^2)，但在这种情况下其实有更高效的解决方案。

以查询最大值为例，对于长度为n的数组a，

$$dp(i, j) 表示从a_i起连续2^j个元素的最大值$$

$$即区间[i, i+2^j-1] 的最大值$$

长度为2^{j区间的最大值可以通过两个长度2}{j-1}的区间最大值得到
所以有状态方程

$$dp(i, j) = max(dp(i, j-1), dp(i+2^{j-1},j-1))$$

对于i=0,1,…,n-1，j取值范围满足 i+2^j<n，即

$$j< log_2(n-i)$$

初始化

我们可以通过递推预处理dp所有的元素，时间复杂度O(nlogn)

查询

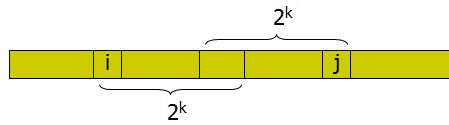
查询区间[i,j]的最大值记作query(i,j)，我们还是可以利用拆分区间的思路把[i,j]拆成两个长度为2^k的区间这样就可以在预处理的dp表里直接找到了。

其中

$$k = \lfloor log_2(j-i+1) \rfloor$$

则

$$query(i,j) = max(dp(i, k), dp(j-2^k+1,k))$$

代码

template<typename T, typename Cmp=less<int>>
class RMQ {
    vector<vector<T>> dp; //dp[i][j]表示从a[i]起连续2^j次方个数的最值

    static int ceil_log2(int n) {
        int r = 0;
        while((1<<r)<n) r++;
        return r;
    }

    static int floor_log2(int n) {
        int r = 0;
        while((1<<r)<=n) r++;
        return r-1;
    }

    int max_or_min(const T& a, const T& b) const {
        return Cmp()(a, b)?a:b;
    }

public:
    RMQ() = default;
    RMQ(const T* a, int n) {init(a, n);}
    RMQ(const vector<T>& a) {init(&a[0], a.size());}

    void init(const T* a, int n) {
        dp.resize(n, vector<T>(ceil_log2(n)+1));
        for(int i=0;i<n;i++){
            dp[i][0] = a[i];
        }
        for(int j=1,s=1;s<n;s=(1<<j++)){
            for(int i=0;i+s<n;i++){
                dp[i][j] = max_or_min(dp[i][j-1], dp[i+s][j-1]);
            }           
        }
    }
    
    //返回[i, j]范围内的最值
    T query(int i, int j) const {
        assert(i<=j);
        int k = floor_log2(j-i+1);
        return max_or_min(dp[i][k], dp[j-(1<<k)+1][k]);
    }
};

template<typename T>
using RMinQ = RMQ<T, less<T>>;
template<typename T>
using RMaxQ = RMQ<T, greater<T>>;